परीक्षण की विश्वसनीयता से आप क्या समझते हैं? (What do you understand by reliability of test?)
परीक्षणों का निर्माण किसी वस्तु, व्यक्ति अथवा क्रियाओं के विभिन्न गुणों का मापन करने के लिए किया जाता है। शिक्षा के क्षेत्र में इनका निर्माण छात्रों के विभिन्न गुणों एवं योग्यताओं (चरों) के मापन के लिए किया जाता है। यदि किसी परीक्षण द्वारा मापीय गुणों का मापन सही ढंग से किया जाता है, उसमें किसी प्रकार की मापन त्रुटि नहीं होती तो ऐसे परीक्षण को विश्वसनीय परीक्षण कहते हैं और उसके इस गुण को विश्वसनीयता कहते हैं। उदाहरण के लिए एक मानकीकृत बुद्धि परीक्षण को लीजिए। यदि हम छात्रों के एक समूह पर उसका प्रशासन आज करते हैं और आज से 10-20 दिन बाद उसी समूह पर पुनः प्रशासन करते हैं और मापन परिणाम समान प्राप्त होते हैं तो ऐसे परीक्षण को विश्वसनीय परीक्षण कहेंगे और उसके इस गुण को विश्वसनीयता कहेंगे।
यह देखा गया है कि कोई भी परीक्षण चर त्रुटियों से पूर्णतः मुक्त नहीं होता। यही कारण है कि विद्वान परीक्षण की विश्वसनीयता का अर्थ उस सीमा से लेते हैं जिस सीमा तक वह चर त्रुटियों से मुक्त होता है। परन्तु गुण को तो गुण के रूप में ही परिभाषित करना चाहिए. न कि उसकी सीमा के आधार पर। एनेस्टेसी महोदय ने इसे गुण के रूप में ही परिभाषित किया है। उनके शब्दों में-
परीक्षण की विश्वसनीयता भिन्न अवसरों पर अथवा समतुल्य पदों के विभिन्न विन्यासों पर किसी व्यक्ति के द्वारा प्राप्त अंकों की संगति बताती है।
स्टोडोला व स्टोर्डल के अनुसार किसी परीक्षण की विश्वसनीयता को उसके विश्वसनीयता गुणांक के रूप में परिभाषित किया जा सकता। उनके शब्दों में-
किसी परीक्षण की विश्वसनीयता को किसी समूह के व्यक्तियों के लिए समतुल्य परीक्षणों पर प्राप्तांकों के दो या दो से अधिक विन्यासों के मध्य विन्यायों के मध्य सहसम्बन्ध के रूप परिभाषित किया जा सकता है।
शैक्षिक मापन कभी भी पूर्ण रूप से विश्वसनीय नहीं हो सकते क्योंकि इनका मापन अप्रत्यक्ष विधियों से किया जाता है और अप्रत्यक्ष विधियों में लाख प्रयत्न के बाद भी मापन त्रुटियाँ होना स्वाभाविक है। यही कारण है कि कुछ विद्वान परीक्षण की विश्वसनीयता को विश्वसनीयता गुणांक के रूप में परिभाषित करते हैं। विश्वसनीयता गुणांक से तात्पर्य वास्तविक प्राप्तांकों के प्रसरण का कुल प्राप्तांकों के प्रसरण के अनुपात से होता है। यहाँ कुल प्रसरण, सत्य प्रसरण एवं त्रुटि प्रसरण का योग है। गणितीय सूत्र द्वारा विश्वसनीयता गुणांक को निम्नलिखित रूप से प्रदर्शित किया जा सकता है-

जिस परीक्षण का विश्वसनीयता गुणांक जितना अधिक होता है वह परीक्षण उतना ही अधिक विश्वसनीय होता है।
विश्वसनीयता एक गुण है और गुण को गुण के रूप में ही परिभाषित करना चाहिए। हमारी दृष्टि में इसे निम्नलिखित रूप में परिभाषित किया जाना चाहिए—
यदि कोई परीक्षण उन मापीय गुणों जिनके मापन के लिए वह बनाया गया है, का सही-सही मापन करता है तो परीक्षण के इस गुण को परीक्षण की विश्वसनीयता कहते हैं।
परीक्षण की विश्वसनीयता ज्ञात करने की विधियाँ
किसी परीक्षण की विश्वसनीयता विश्वसनीयता गुणांक द्वारा ज्ञात की जाती है। विश्वसनीयता गुणांक ज्ञात करने की अनेक विधियाँ है उनमें से मुख्य विधियाँ निम्नलिखित हैं-
1. परीक्षण-पुनर्परीक्षण विधि (Test- Retest Method)- इस विधि में एक परीक्षण को दो विभिन्न अवसरों पर एक ही समूह पर प्रशासित किया जाता है। फिर दोनों अवसरों के प्राप्तांकों में सहसम्बन्ध ज्ञात किया जाता है। यह सहसम्बन्ध गुणांक ही विश्वसनीय गुणांक होता है। इसे स्थिरता गुणांक भी कहते हैं। यह गुणांक जितना अधिक होता है, परीक्षण उतना ही अधिक विश्वसनीयता होता है। इन दो अवसरों के प्राप्तांकों का सहसम्बन्ध गुणांक निम्नलिखित सूत्र द्वारा ज्ञात किया जाता है-

यह विधि सर्वाधिक प्रचलित विधि है। यह प्रशासन, अंकन एवं गणना में सरल है। लेकिन इसकी अपनी सीमाएँ हैं। इस विधि में एक ही परीक्षण को कुछ समय के अन्तराल से दो बार प्रशासित किया जाता है अतः विश्वसनीयता पर अभ्यास, स्मृति, व्यक्ति के अन्दर होने वाले परिवर्त्तनों, क्षमताओं में वृद्धि सवं परीक्षण को दो बार प्रशासित करने के मध्य जितना अधिक समय होगा उतना ही उपर्युक्त तत्त्वों का प्रभाव विश्वसनीयता गुणांक पर पड़ेगा। और अत्यन्त ही कम समय में प्रशासित करने पर वे ही प्राप्तांक प्राप्त हो सकते हैं जो पहली बार प्रशासन करते समय प्राप्त हुए थे। अतः परीक्षण की प्रकृति के अनुसार इस समयान्तराल को निश्चित करना चाहिए ताकि शुद्ध परिणाम मिल सकें।
2. समान प्रारूप विधि (Parallel Form Method)- इस विधि में एक परीक्षण के दो समानान्तर रूप तैयार किए जाते हैं। सर्वप्रथम एक रूप को एक समूह पर प्रशासित कर उसके प्राप्तांकों को प्राप्त किया जाता है। कुछ समय पश्चात् उसी समूह पर परीक्षण के दूसरे रूप को प्रशासित किया जाता है और उसके प्राप्तांकों को प्राप्त किया जाता में इस प्रकार प्राप्त प्राप्तांकों में सहसम्बन्ध ज्ञात किया जाता है। यही सहसम्बन्ध इस परीक्षण । अन्त का विश्वसनीयता गुणांक होता है। यह मान जितना अधिक होता है, परीक्षण उतना ही अधिक विश्वसनीय होता है इस विश्वसनीयता गुणांक को तुल्यता गुणांक भी कहते हैं।
इस विधि की प्रमुख विशेषता यह है कि इसमें अभ्यास, स्मृति आदि का प्रभाव कम पड़ता है क्योंकि परीक्षण के दोनों रूपों के पदों का स्वरूप तो एक सा होता है लेकिन पद भिन्न होते हैं।
3. अर्द्ध विच्छेद विधि (Split-half Method) – इस विधि में परीक्षण के समस्त पदों को दो बराबर भागों में विभाजित किया जाता है। इन दो बराबर भागों को एक ही समय में एक ही समूह पर प्रशासित कर प्राप्तांक प्राप्त किए जाते हैं। इन दो प्राप्तांकों के समूह के मध्य सहसम्बन्ध ज्ञात किया जाता है। यह सहसम्बन्ध परीक्षण का अर्द्ध विश्वसनीयता गुणांक कहलाता है। सम्पूर्ण परीक्षण का विश्वसनीयता गुणांक प्राप्त करने के लिए स्पीयरमेन ब्राउन के निम्नांकित सूत्र का प्रयोग किया जाता है-

चूँकि यह परीक्षण दो बराबर भागों में विभाजित किया जाता है इसलिए परीक्षण की लम्बाई घट जाती हैं जिसके कारण इसकी विश्वसनीयता कम हो जाती है। लम्बाई के प्रभाव से बचने के लिए स्पीयरमेन ब्राउन ने अपने सूत्र में संशोधन कर सम्पूर्ण परीक्षण का विश्वसनीयता गुणांक ज्ञात करने के लिए नया सूत्र दिया जो निम्नांकित है-

इस विधि में मुख्य बात यह है कि परीक्षण को दो समान भागों में विभक्त किया जाता है साधारणतः प्रत्येक परीक्षण का निर्माण कठिनता स्तर के अनुसार बढ़ते क्रम में किया जाता है और इस प्रकार उसे दो बराबर भागों में विभक्त कर दिया जाता है। परन्तु इस प्रकार से प्राप्त दोनों भाग विषय-वस्तु, कठिनता स्तर एवं अन्य बाह्य कारणों से समान नहीं होते हैं। अतः परीक्षण की सर्वसम्भव समान दो भागों में विभक्त करने के लिए इसके सम एवं विषम पदों को अलग किया जाता है। एक भाग में परीक्षण के सभी विषय संख्या पद और दूसरे भाग में परीक्षण के सभी सम संख्या पद लेते हैं। इन दोनों भागों को एक ही समूह पर प्रशासित कर प्राप्तांक प्राप्त किए जाते हैं और इसके बाद इन दोनों समूहों के प्राप्तांकों के मध्य सहसम्बन्ध, जिसे अर्द्ध विश्वसनीयता गुणांक ज्ञात किया जाता है। 53 इस विधि का मुख्य गुण यह है कि इसमें विश्वसनीयता की गणना के लिए आवश्यक निदर्श एक ही अवसर पर प्राप्त हो जाते हैं और प्रत्येक अर्द्ध भाग का प्रशासन भी एक ही बार होता है अतः अभ्यास एवं स्मृति का प्रभाव विश्वसनीयता पर नहीं पड़ता।
इस विधि का मुख्य गुण यह है कि इसमें विश्वसनीयता की गणना के लिए आवश्यक निदर्श एक ही अवसर पर प्राप्त हो जाते हैं और प्रत्येक अर्द्ध भाग का प्रशासन भी एक ही बार होता है अतः अभ्यास एवं स्मृति का प्रभाव विश्वसनीयता पर नहीं पड़ता ।
इस विधि में एक कमी भी है। इसमें परीक्षण को कई विधियों से दो समान भागों में बाँटा जा सकता है अतः अलग-अलग विधियों से प्राप्त अर्द्ध विच्छेदों का सहसम्बन्ध भी अलग-अलग आता है।
4. तर्कयुक्त समानता विधि (Method of Rational Equivalence)- इस विधि को कूडर रिचर्डसन विधि के नाम से भी जाना जाता है। इस विधि में परीक्षण के विभिन्न पदों का आपस में सम्बन्ध एवं पदों का सम्पूर्ण परीक्षण से सहसम्बन्ध ज्ञात किया जाता है। इसे आन्तरिक संगति गुणांक कहा जाता है। इस विधि की मुख्य मान्यता यह है कि परीक्षण ऐसा होना चाहिए जो केवल एक ही गुण का मापन करे। इस विधि में परीक्षण के प्रश्नों को छात्रों द्वारा दिए गए उत्तरों की संगतता के सन्दर्भ में देखा जाता है। यदि परीक्षण के प्रश्नों को कठिनाई स्तर के बढ़ते क्रम में व्यवस्थित किया जाए तो आदर्श स्थिति में प्रत्येक छात्र एक ऐसे बिन्दु पर पहुँचेगा, जिससे पहले के सभी प्रश्नों को वह सही हल करेगा और बाद के सभी प्रश्नों को सही हल नहीं कर सकेगा। यदि सभी छात्रों के लिए ऐसा विभाजन सम्भव होता है तो परीक्षण पूर्ण रूप से विश्वसनीय होगा। वास्तविक विश्वसनीयता को ज्ञात करने के लिए कूडर द्वारा दिए गए निम्नांकित सूत्र को प्रयोग किया जाता है, क्योंकि वास्तविक स्थिति में प्रश्नों की कठिनाई के अनुरूप विभिन्न छात्रों के लिए सही तथा गलत में विभाजित करने वाले बिन्दु भिन्न-भिन्न होंगे।

विश्वसनीयता ज्ञात करने के लिए उपर्युक्त सूत्र में प्रत्येक प्रश्न या पद के लिए सही एवं गलत उत्तरों की संख्या की जानकारी आवश्यक है। इस कारण गणना कार्य जटिल होता है। यदि सभी प्रश्नों का कठिनाई स्तर लगभग समान हो तो उपर्युक्त सूत्र निम्नांकित रूप में लिखा जा सकता है-

इस विधि में सर्वप्रथम छात्रों पर परीक्षण प्रशासित कर उन्हें अंक प्रदान किए जाते हैं। फिर इन प्राप्तांकों का मानक विचलन (σ) ज्ञात किया जाता है। इसके साथ ही सभी छात्रों ने प्रत्येक पद को किस-किस अनुपात में सही हल किया है, उसका मापन कर p एवं q का मान निर्धारित किया जाता है। सभी pq के गुणा का योग कर Σpq ज्ञात किया जाता है। फिर सूत्र की सहायता से विश्वसनीयता गुणांक ज्ञात किया जाता है।
इस विधि से विश्वसनीयता गुणांक ज्ञात करने से अन्य विधियों के दोषों को दूर किया जा सकता है। इस विधि की सबसे बड़ी विशेषता यह है कि इसमें परीक्षण का प्रत्येक पद उच्च सहसम्बन्ध रखता है किन्तु यदि पद सजातीय नहीं हुए तो सहसम्बन्ध का मान निम्न हो सकता है।
5. होय्ट विधि (Hoyt’s Method) — होय्ट ने विश्वसनीयता ज्ञात करने की एक विध का विकास किया है जिसके परिणाम कूडर रिचर्डसन विधि के परिणाम के समान होते हैं। होय्ट के अनुसार किसी व्यक्ति की विभिन्न प्रश्नों को हल करने की योग्यता में अन्तर होता है । इस अन्तर को त्रुटि नहीं माना जा सकता, वरन् यह एक वास्तविक अन्तर होता है जिसे अन्तः व्यक्ति अन्तर कहते हैं। होय्ट ने विश्वसनीयता गुणांक ज्ञात करने के लिए प्रसरण का उपयोग किया । उसके अनुसार कुल प्रसरण को तीन भागों में विभाजित किया जाता है- एक सत्य प्रसरण, दूसरा पद प्रसरण एवं तीसरा त्रुटि प्रसरण।
सत्य प्रसरण छात्रों के प्राप्तांकों का वास्तविक प्रसरण होता है जिसे σ²t से प्रदर्शित किया जाता है। पद प्रसरण पदों अथवा प्रश्नों पर प्राप्तांकों के लिए प्रसरण होता है जिसे σ²i द्वारा प्रदर्शित किया जाता है तथा त्रुटि प्रसरण चर त्रुटि के अंकों का प्रसरण होता है जिसे σ²e द्वारा प्रदर्शित किया जाता है। समीकरण के रूप में इसे निम्नांकित रूप में लिखा जाता है—
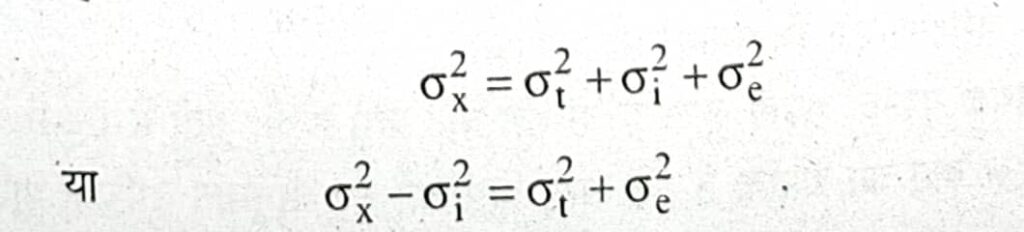

इस विधि से प्राप्त विश्वसनीयता गुणांक तर्कयुक्त समानता विधि से कम आता है लेकिन सैद्धान्तिक दृष्टि यह एक उत्तम विधि है। इस विधि में अन्य विधियों की कमियों को दूर किया गया है।
6. मापन की मानक त्रुटि विधि (Standard Error of Measurement Method)— परीक्षण की विश्वसनीयता को मापन की मानक त्रुटि द्वारा भी ज्ञात किया जा सकता है। इसके द्वारा यह अनुमान लगाया जाता है कि किसी परीक्षण के प्राप्त अंकों तथा उसके वास्तविक या सत्य प्राप्तांकों में कितना विचलन है। यही अन्तर मापन की त्रुटि होती है। इस विधि में पहले किसी विधि से विश्वसनीयता गुणांक ज्ञात कर लिया जाता है। साथ ही प्राप्त प्राप्तांकों का मानक विचलन ज्ञात कर निम्नांकित सूत्र की सहायता से मापन की मानक त्रुटि ज्ञात की जाती है-

जैसे-जैसे विश्वसनीयता गुणांक बढ़ता जाता है, मानक त्रुटि कम होती जाती है। अधिक विश्वसनीयता का होना इस बात का द्योतक है कि सत्य प्राप्तांकों का अनुमान अधिक शुद्ध है तथा अन्तर-बाह्य तत्त्वों के कारण सत्य प्राप्तांकों एवं प्राप्त प्राप्तांकों का विचलन कम है।, निम्नांकित सूत्र का प्रयोग कर प्राप्त प्राप्तांकों के विश्वसनीयता गुणांक द्वारा सत्य प्राप्तांकों का विश्वसनीयता गुणांक ज्ञात किया जा सकता है—

परीक्षण की विश्वसनीयता परीक्षण पदों की संख्या बढ़ाकर एवं विभिन्न स्रोतों से हुई त्रुटियों को कम करके बढ़ाई जा सकती है।
यह विधि यह इंगित करती है कि परीक्षण प्राप्तांकों से प्राप्त विश्वसनीयता गुणांक सत्य प्राप्तांकों के विश्वसनीयता गुणांक के कितना नजदीक है । मापन की मानक त्रुटि के प्राप्तांकों का वितरण प्रायः सामान्य वक्र के आधार पर होता है अतः इससे प्राप्त परिणाम समष्टि के लिए उपयोगी होते हैं।
इसे भी पढ़े…
- पाठ्यचर्या विकास की प्रक्रिया
- पाठ्यचर्या निर्माण के लिए शिक्षा के उद्देश्य
- पाठ्यक्रम निर्माण के सिद्धान्त
- पाठ्यक्रम निर्माण के सामाजिक सिद्धान्त
- पाठ्यक्रम के प्रमुख निर्धारक
- पाठ्यक्रम विकास के मुख्य प्रसंग
- मानसिक मंदता से सम्बद्ध समस्याएँ
- विकलांगजन अधिनियम 1995
- सक्षम निःशक्तजनों का राष्ट्रीय संगठन
- मानसिक मंदित बालकों की पहचान
- शिक्षण अधिगम असमर्थता एवं शैक्षिक प्रावधान
- श्रवण अक्षमता क्या है? इसकी व्यापकता
- श्रवण अक्षमता के कारण






