Two’s Complement: Definition, Conversion, Addition, Subtraction, and Examples

The term two’s complement is a wide concept in the IT department. It is a well-known operation of binary variables. In mathematical manipulation, the two’s complement is a way to record the operation on binary numbers.
It is helpful in defining the positive and negative numbers in binary. It is frequently used in the coding of computers and calculators. It was used by John von Neumann in the 1950s for the first time while he was writing on EDSAC and EDVAC computers.
This evaluation of the two’s complement opens the way for mathematical abstractions of numbers that can be used for computing purposes like machine coding. In this post, we will learn the conversion, addition, and subtractions of two’s complement with examples.
What is the two’s complement?
A system that encodes negative and positive numbers in binary number representation is said to be the two’s complement. The two’s complement can also be described by the experts as a binary signed number representation.
The signed representation has to do with signed and unsigned values for 8, 12, and 16-bit binary numbers or other bit-system of binary numbers. The bit is helpful in the basic explanation of computing, encoding, or telecommunications.
A single unit of digital information represent in zero or one is known as a bit. The bits are very essential for encoding data. The power full bit system must be 2 to the power of. Firstly, the one’s complement was used for computing purposes but it was only applicable to positive integers.
So, a two’s complement was coming into being as it is helpful in encoding both positive and negative integers. Let’s further explore the conversions of binary and decimal numbers into two’s complements.
Conversions of binary and decimals into 2s complement
Here we are going to learn how to convert a binary or decimal number into two’s complement.
- Converting a Binary Number into 2s Complement
Below are a few steps that will help you to understand how to convert a binary number into a twos complement.
-
- First of all, write the given binary number.
- Invert all the zeros of the binary number in ones and all the ones in zeros. The process of inverting zeros into ones and ones into zeros is said to be the one’s complement of a binary number.
- Now add 1 to the right-most bit of the 1’s complement to get the result of the two’s complement of the given binary number.
- Converting a Decimal Number into 2s Complement
Below are a few steps that will help you to understand how to convert a decimal number into a two’s complement.
- First of all, take the given decimal number and convert it into a binary number.
- Complete the bit system by adding zeros to the leftmost side.
- Invert all the zeros of the binary number in ones and all the ones in zeros. The process of inverting zeros into ones and ones into zeros is said to be the one’s complement of a binary number.
- Now add 1 to the right-most bit of the 1’s complement to get the result of the two’s complement of the given binary number.
Addition and Subtraction of two’s complement
The arithmetic operations like addition and subtraction of two’s complement follow the basic laws or rules of binary arithmetic. There are four possible tricks for the addition and subtractions of two’s complement.
- If both numbers are positive, then the result will be positive.
- If a positive number with smaller magnitude than a negative number, then the result will be negative.
- If a positive number with a larger magnitude than a negative number, then the result will be positive.
- If both numbers are negative, then the result will be negative.
Examples of two’s complement
Here are a few examples of two’s complement.
Example 1: For the binary conversion into 2s complement.
Convert the given binary variable into a signed number representation.
101100101010
Solution
Step 1: First of all, write the given binary variable number.
101100101010
Step 2: Now find the 1s complement of the given binary number by inverting all the zeros to ones and ones to zeros.
010011010101
Step 3: Now to get the two’s complement of the given binary number, add 1 to the rightmost side of the above term.
0 1 0 0 1 1 0 1 0 1 0 1
+ 1
0 1 0 0 1 1 0 1 0 1 1 0
Hence,
The 2s complement of “101100101010” is “010011010110”
Example 2: For converting a decimal into a 2s complement
Convert the given decimal variable into a signed number representation.
415
Solution
Step 1: First of all, write the given decimal number.
415
Step 2: Now convert the given decimal number into the binary variable form.
| 2 | 415 |
| 2 | 207 – 1 |
| 2 | 103 – 1 |
| 2 | 51 – 1 |
| 2 | 25 – 1 |
| 2 | 12 – 1 |
| 2 | 6 – 0 |
| 2 | 3 – 0 |
| 1 – 1 |
Hence,
415 = (110011111)2
Step 3: Now complete the nearest-bit system by adding zeros to the leftmost side.
000110011111
Step 4: Now find the 1s complement of the given binary number by inverting all the zeros to ones and ones to zeros.
111001100000
Step 5: Now to get the two’s complement of the given binary number, add 1 to the rightmost side of the above term.
1 1 1 0 0 1 1 0 0 0 0 0
+ 1
1 1 1 0 0 1 1 0 0 0 0 1
Hence,
The 2s complement of “415” is “111001100001”
You can try a 2s complement calculator by AllMath to avoid confusing calculations of conversions of binary variables or decimal numbers.
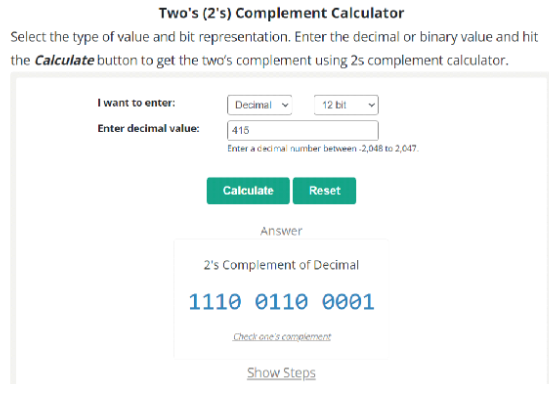
Solved by two’s complement calculator by AllMath
Example 3: For the addition of two’s complement.
Find the two’s complement of 5 and 9 and add the two’s complement.
Solution
Step 1: First of all, convert the given decimals to binary numbers.
For 5
| 2 | 5 |
| 2 | 2 – 1 |
| 2 | 1 – 0 |
For 9
| 2 | 9 |
| 2 | 4 – 1 |
| 2 | 2 – 0 |
| 1 – 0 |
Step 2: Now complete the nearest-bit system by adding zeros to the leftmost side.
5 = (00000101)2
9 = (00001001)2
Step 3: Now find the 1s complement of the given binary number by inverting all the zeros to ones and ones to zeros.
5 = (00000101)2 = 11111010
9 = (00001001)2 = 11110110
Step 4: Now to get the two’s complement of the given binary number, add 1 to the rightmost side of the above term.
5 = (00000101)2 = 11111010 + 1 = 11111011
9 = (00001001)2 = 11110110 + 1 = 11110111
Step 5: Now add the two’s complement of 5 and 9.
1 1 1 1 1 0 1 1
+ 1 1 1 1 0 1 1 1
1 1 1 1 1 0 0 1 0
Example 4: For subtraction of two’s complement.
Find the two’s complement of 7 and 11 and subtract the two’s complement.
Solution
Step 1: First of all, convert the given decimals to binary numbers.
For 7
| 2 | 7 |
| 2 | 3 – 1 |
| 2 | 1 – 1 |
For 11
| 2 | 11 |
| 2 | 5 – 1 |
| 2 | 2 – 1 |
| 1 – 0 |
Step 2: Now complete the nearest-bit system by adding zeros to the leftmost side.
7 = (00000111)2
11 = (00001011)2
Step 3: Now find the 1s complement of the given binary number by inverting all the zeros to ones and ones to zeros.
7 = (00000111)2 = 11111000
11 = (00001011)2 = 11110100
Step 4: Now to get the two’s complement of the given binary number, add 1 to the rightmost side of the above term.
7 = (00000111)2 = 11111000 + 1 = 11111001
11 = (00001011)2 = 11110100 + 1 = 11110101
Step 5: Now subtract the two’s complement of 7 and 11.
1 1 1 1 1 0 0 1
– 1 1 1 1 0 1 0 1
0 0 0 0 0 1 0 0
Hence 7 – 11 = (11111001)2 – (11110101)2 = 100
Summary
Now you can take the assistance of conversion, addition, and subtraction of two’s complement from this post. As we have discussed all the terms briefly with solved examples. Once you learned the basic criteria of two’s complement, you will master it.



